つるかめ算は、中学受験で登場する文章題の代表格です。
「つると亀が合わせて◯匹、足の合計が◯本」という条件から、それぞれの数を求める問題ですが、いざ解こうとすると混乱してしまう人も少なくありません。
この記事では、つるかめ算の解き方を表・線分図・面積図の3パターンで丁寧に解説します。
算数が苦手な人でも理解できるよう、例題を使って手順を分かりやすく説明しているので、初めて学習する方や復習したい方におすすめです。
つるかめ算とは?
算数の文章題の代表格
つるかめ算は、昔から小学校の算数や中学受験の文章題でよく出題される有名な問題です。
「つる」と「かめ」という二種類の動物(または物)を使って、合計の数と合計の足の数などの条件から、それぞれの数を求めます。
文章を正しく読み取り、条件を整理する力を養うのに最適な問題です。
「つる」と「かめ」の条件から数を求める問題
例えば、
つると亀が合わせて15匹いて、足の数の合計は46本です。つるは何羽いますか?
というように、2種類のものについて、合計の数と合計の量(足の数・金額・時間など)が与えられます。
つる(足2本)とかめ(足4本)のように、1つあたりの値が異なるため、その差を利用して求めるのがポイントです。
中学受験・算数の基礎にも必須
つるかめ算は、中学受験では基礎中の基礎として押さえておくべき単元です。
単純な動物の足の数の問題だけでなく、料金・時間・面積などに応用される「応用型つるかめ算」も頻繁に出題されます。
表・線分図・面積図など複数の解き方を知っておくことで、応用問題にも対応できるようになります。
例題|つる15匹と亀の合計が46本の足
今回の例題は、つるかめ算の中でも最も基本的なタイプです。
つると亀が合わせて15匹います。足の合計は46本です。つるは何羽いますか?
つるは1羽あたり足が2本、亀は1匹あたり足が4本です。
この条件をもとに、「つるが何羽で、亀が何匹か」をを表・線分図・面積図の3つの方法で解いてみます。
表を使ったつるかめ算の解き方
ツルの数、カメの数、足の合計の一覧表
まずは、次のような表を描きます。
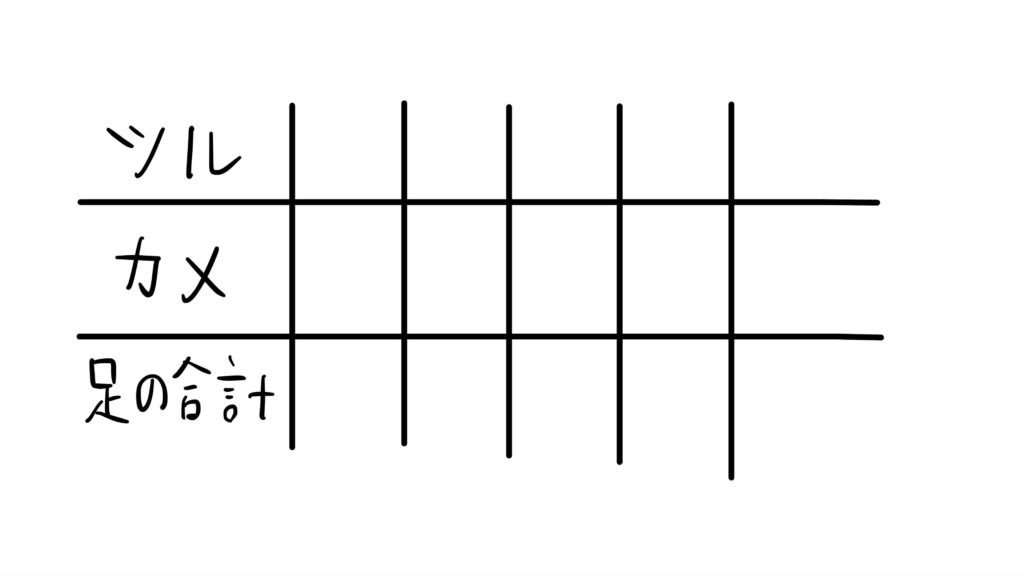
ツルの数(羽)を求めたいなら、全てカメだとみなす
今回の問題ではツルの数を求めます。
鶴と亀合わせて15匹を、すべて亀だとみなして下のように「ツル0」「カメ15」と書き込みます。
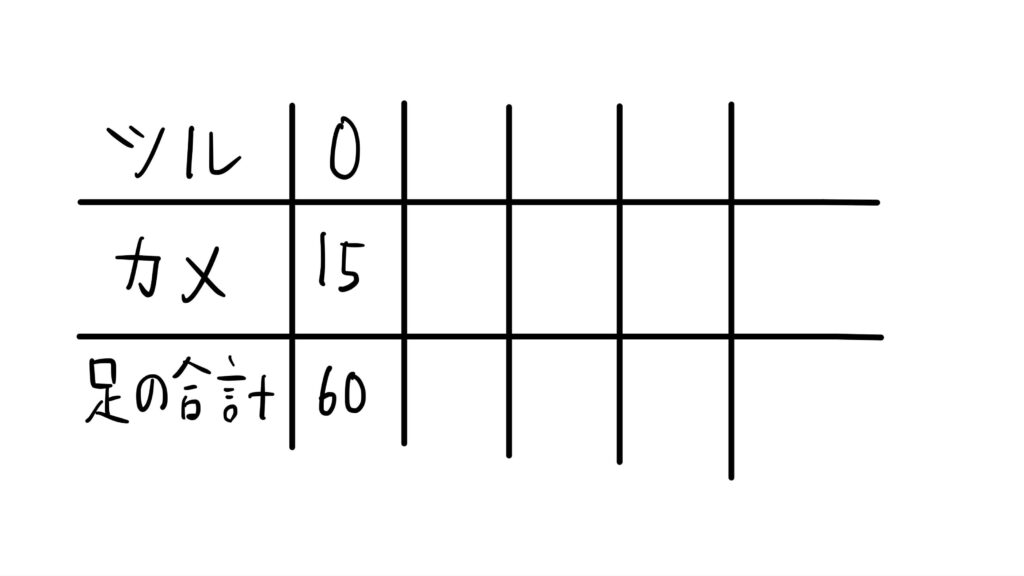
このとき、ツルとカメの足の合計は、
2×0+4×15=60(本)
「15羽すべてツル」とみなして解くこともできます。
その場合、まずカメの数を求めます。
そして、ツルの数=15ーカメの数となります。
ツルを増やしてカメを減らしていく
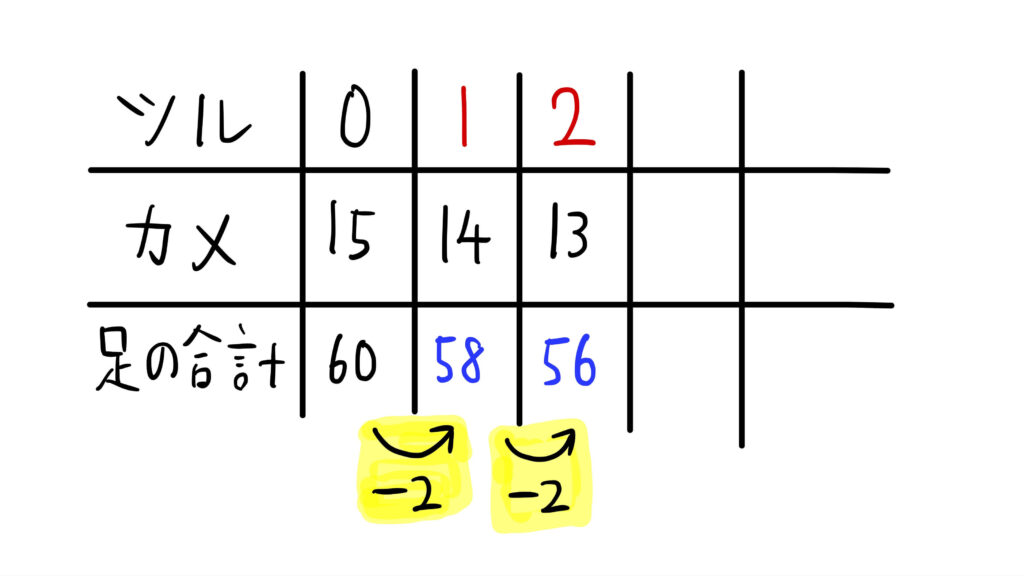
ここで、ツルを1羽増やすと、カメは1匹減って14匹になります(※ツルとカメは合わせて15匹)。
このとき、足の合計は、
2×1+4×14=58(本)
さらに、ツルを1羽増やし、カメを1匹減らすと「ツル2羽、カメ13匹」となります。
このとき、足の合計は、
2×2+4×13=56(本)
ツルを1羽増やすごとに、足の合計は2本減る
表を見ると、「ツルを1羽増やすごとに、足の合計は2本減る」ことがわかります。
「ツル0羽、足の合計60本」
「ツル1羽、足の合計58本」
「ツル2羽、足の合計56本」
・・・
足の合計46本のとき、ツル□羽とする
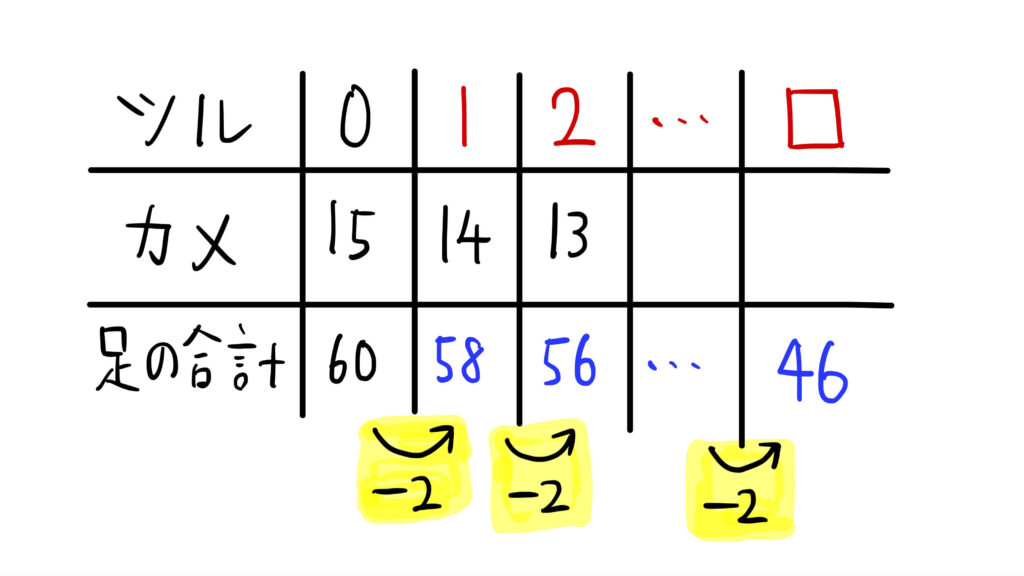
表から、
足の合計=60ーツルの数×2
となっていることがわかります。
よって、ツルが□羽のとき、足の合計は46本なので、
46=60ー□×2
これを解くと、
□×2=60ー46
□×2=14
□=14÷2=7
したがって、求めるツルの数は7羽。
線分図を使ったつるかめ算の解き方
足の数を「線の長さ」で表す
今回は、ツルの数を求めたいので、全員をカメにすると足の合計は60本。
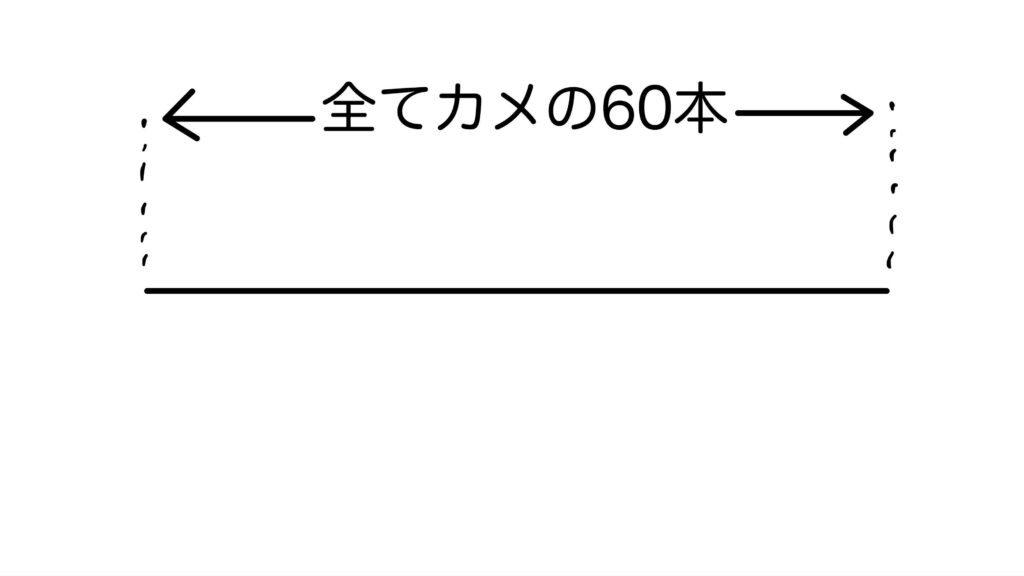
表で解く方法と同様、「15羽すべてツル」とみなして解くこともできます。
その場合、まずカメの数を求めることになります。
カメを減らしてツルを増やしていく
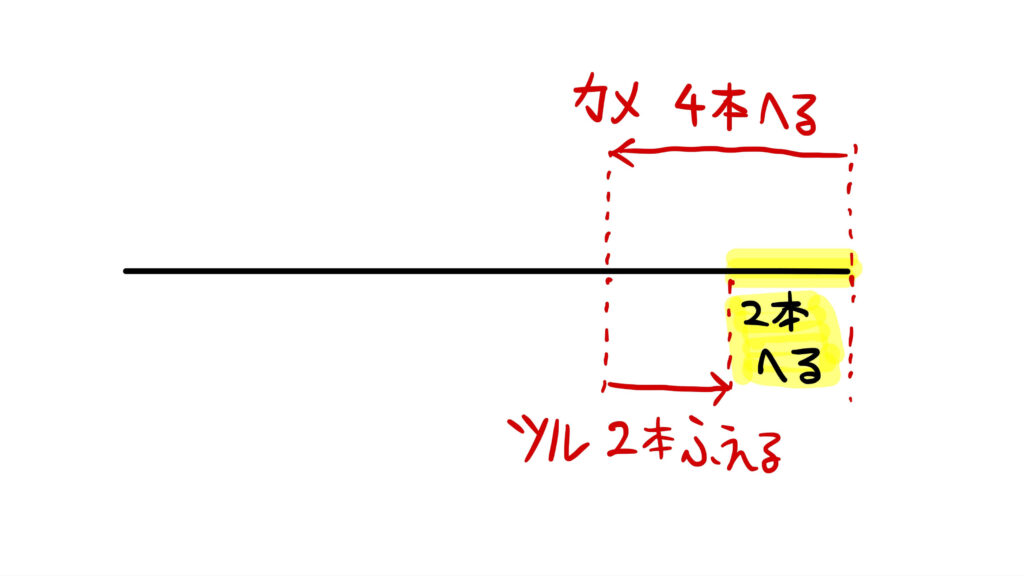
カメを1匹減らすと足の数は4本減ります。
しかし、それと同時にツルを1羽増やすことで、足の数は2本増えます。
よって、カメとツルを1匹とりかえるごとに、足の合計は2本減ることがわかります。
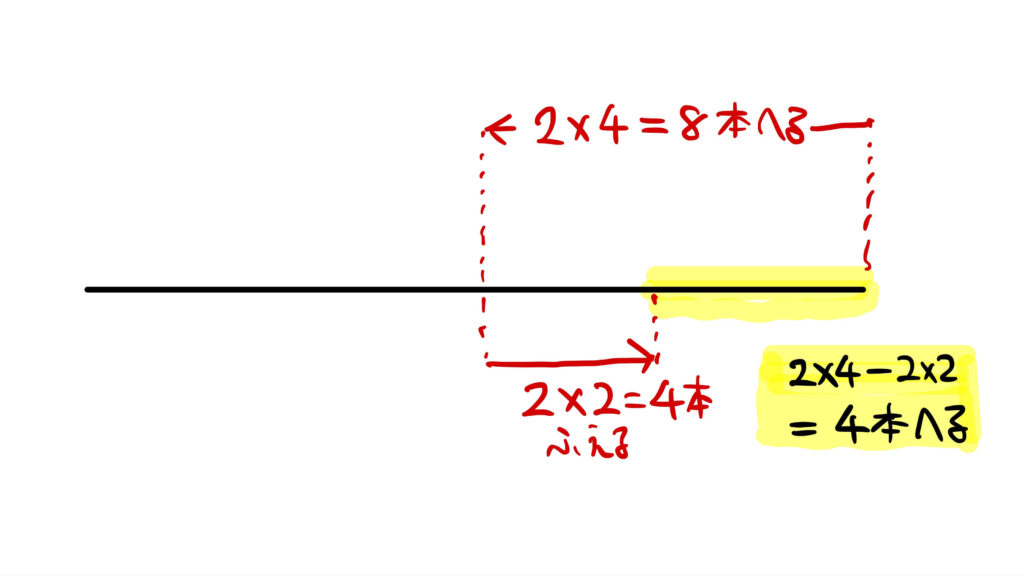
同様にして、
2匹とりかえると2×4ー2×2=4本減る、
3匹とりかえると3×4ー3×2=6本減る、
・・・
ということがわかります。
ツルが□羽のときの線分図
すると、□匹とりかえると□×4ー□×2=□×(4-2)=□×2本減ることになります。このとき足の合計は46本です。
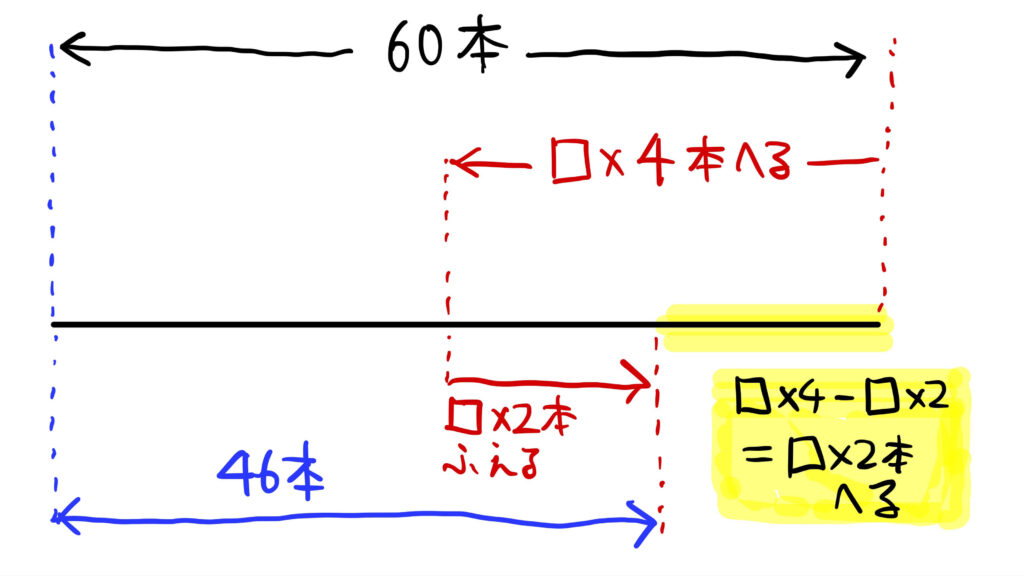
□×2=60ー46
□=14÷2=7(羽)
面積図を使ったつるかめ算の解き方
縦を1匹あたりの足の数、横を匹数として面積を考える
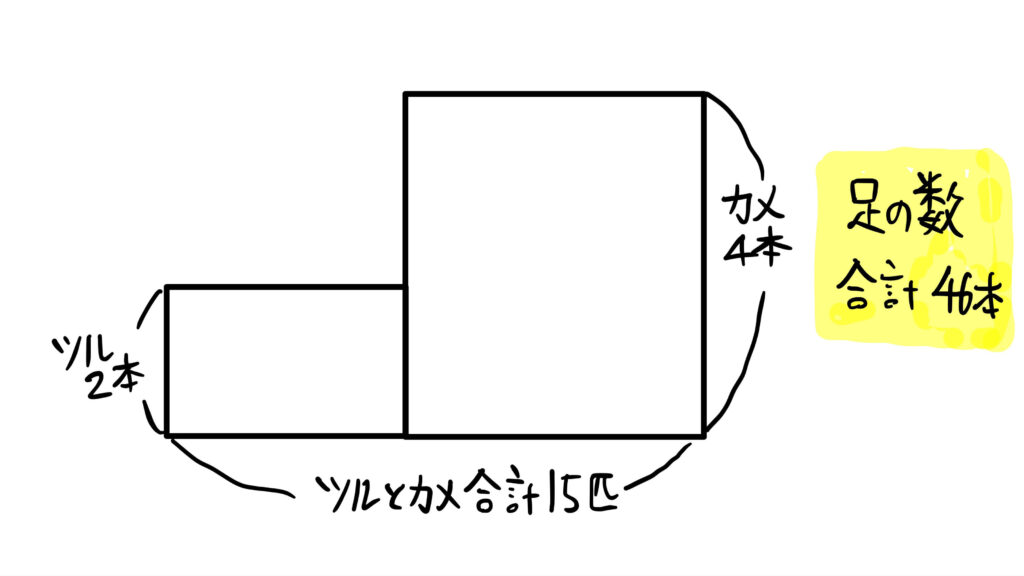
縦=1匹の足の本数、横=匹数として長方形の面積を「足の合計」として表します。
- かめ:縦4(足4本)
- つる:縦2(足2本)
全体面積と差を利用して求める
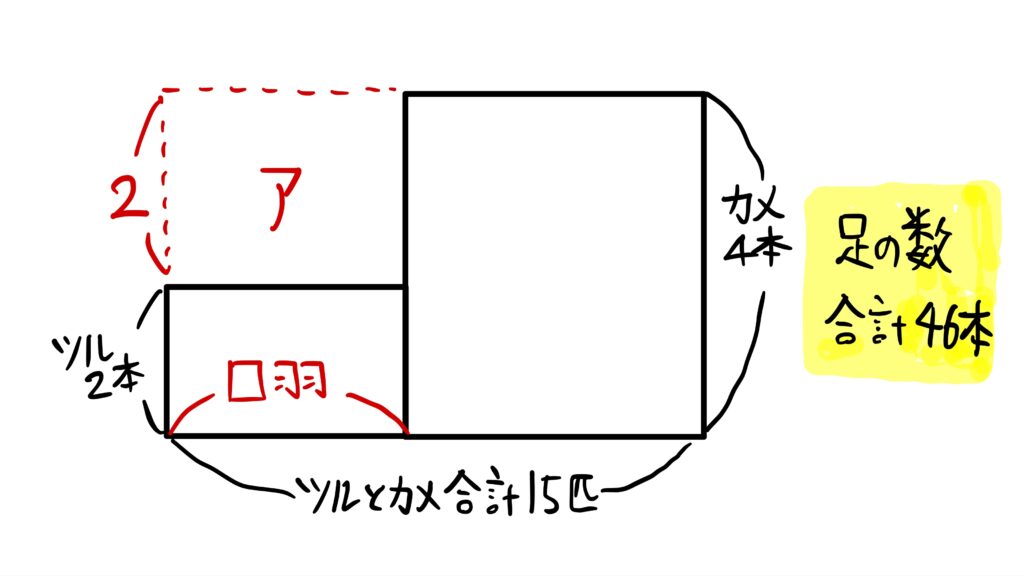
今回は、ツルの数を求めたいので、ツルの数を□羽とします。
そして、面積アに注目すると、次の式が作れます。
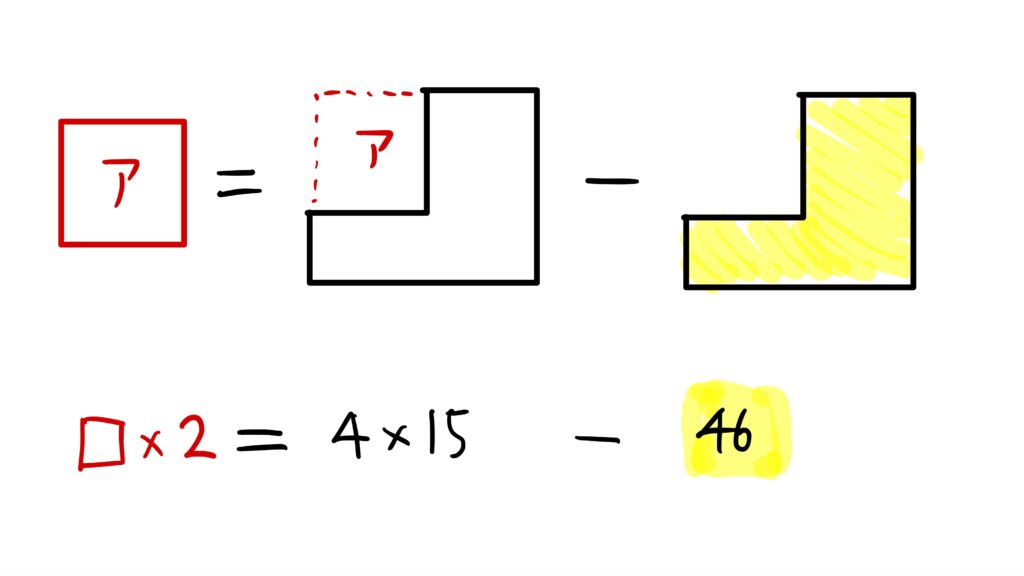
□×2=4×15ー46
□×2=60ー46=14
□=14÷2=7(羽)
まとめ|初心者は面積図から、応用は表・線分図も活用しよう
小学校4年生向けのテキストでは、「表で解く方法」や「取り替える方法(線分図)」が最初に解説されていることが多いですが、はじめてつるかめ算を学習する人にはややわかりにくいことがあります。
そんなときは、面積図から学習するのがおすすめです。
面積図は直感的でわかりやすく、理科の「金属の酸化」など計算問題にも応用できます。
面積図に慣れたら、次は表や線分図もマスターしましょう。
応用レベルのつるかめ算では、面積図だけでは解きにくい問題もあり、表や線分図を使ったほうがスムーズに解けるケースも多いです。
ステップアップの流れ
- 初心者は面積図で理解する
- 慣れてきたら表・線分図も練習する
この順番で学べば、つるかめ算の解き方を幅広くマスターでき、文章題への対応力が大きく伸びますよ!


