問題文
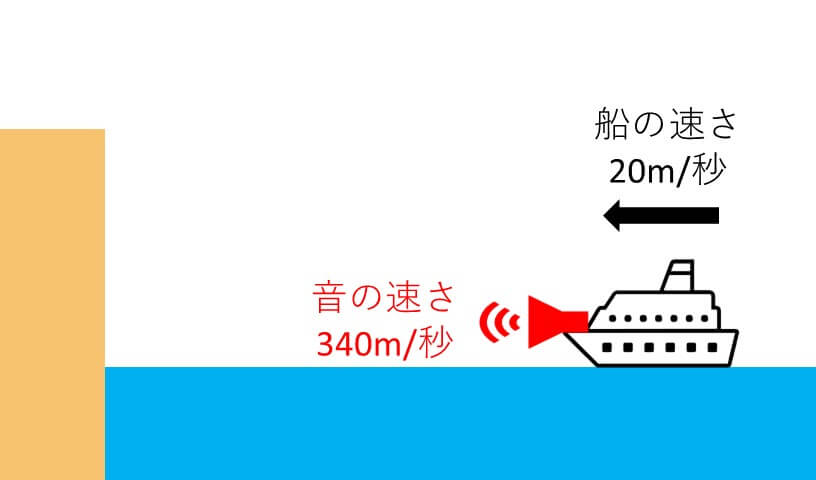
音速が秒速340m、船の速さが秒速20m のとき、船は 3秒間 汽笛を鳴らし続けます。
このとき、船に乗っている人が 岸壁で反射して返ってくる汽笛の音 を聞いていた時間を求めなさい。割り切れない場合は、小数第一位までもとめなさい。
(1)船が 海から岸壁に向かっている場合
(2)船が 岸壁から離れていく場合
解答のポイント
「音を聞いていた時間」だけを求める場合、「船と岸壁の距離」はわからなくてもいいです。以下が解答のポイントです。
- 船と岸壁の距離は分からなくてもOK
- 「船にいる人が反射音を聞いた時間」=「はじめの音を聞いてから、おわりの音を聞くまでの時間」
- 「はじめの音とおわりの音の間の長さ」を列車に見立てる
- 列車と船の「通過算」として計算
それでは、(1)(2)それぞれの場合について図解を添えて解説します。
解答(1)船が岸壁に向かっている場合
3秒後の位置を作図
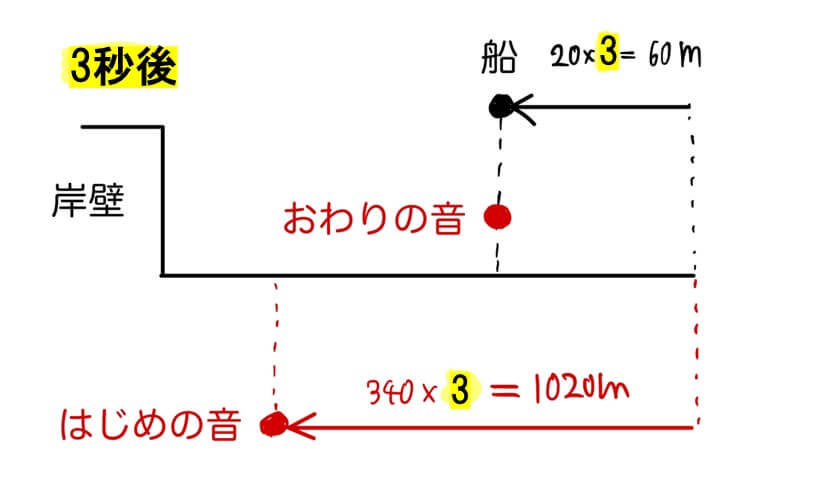
船は3秒間汽笛を鳴らしたことに注目。
汽笛を鳴らして3秒後の「船」「はじめの音」「終わりの音」の位置関係を作図します。
すると、音の長さ(はじめの音から、おわりの音までの長さ)を列車の長さと見なすことができます。
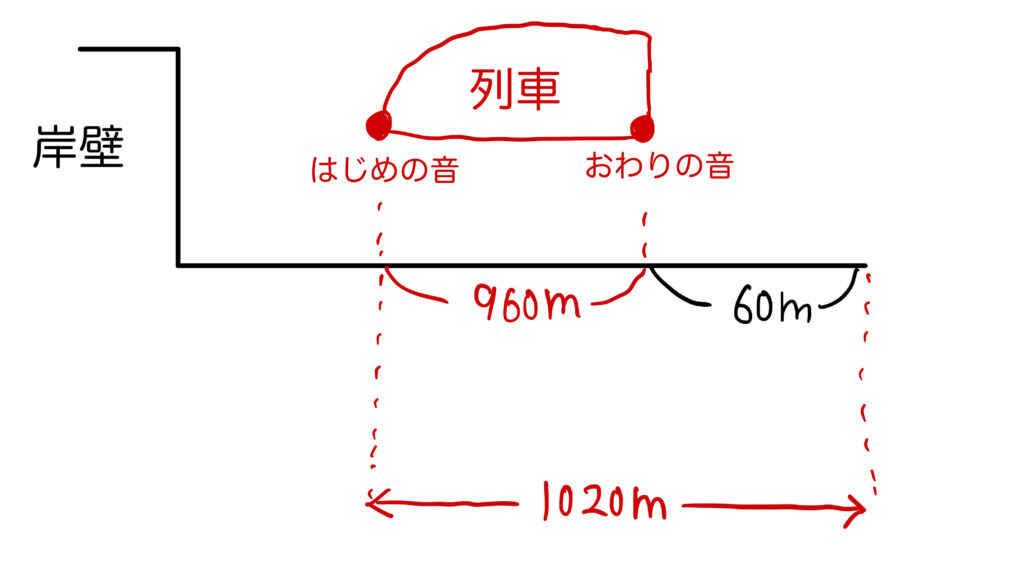
列車と船の通過算(出会い)
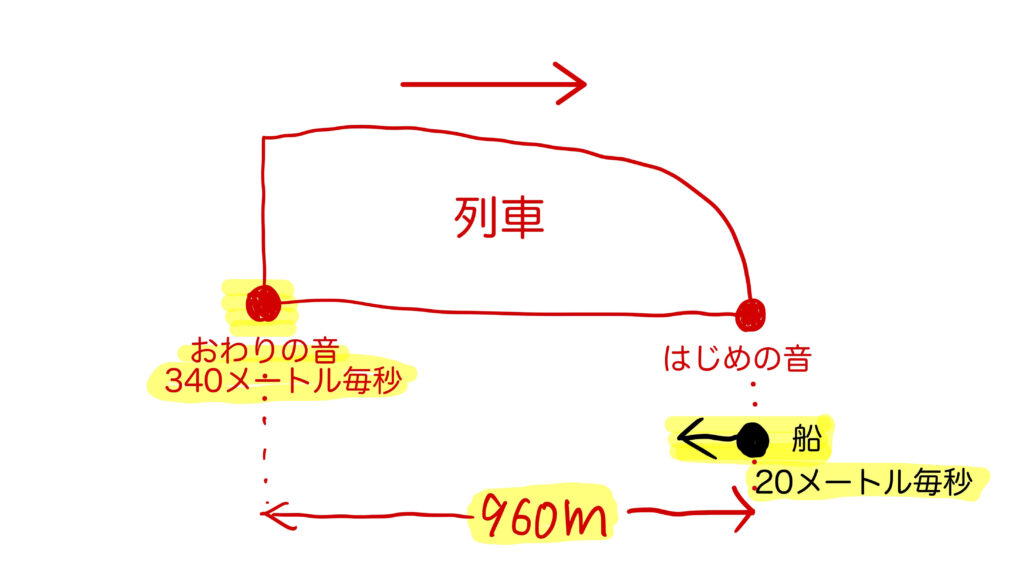
「船に乗っている人が反射音を聞いていた時間」は、「列車(960m)と船(0m)がすれちがう時間」となります。
すれ違う時間=(列車の長さ+船の長さ)÷(列車の速さ+船の速さ)なので、
(960+0)÷(340+20)=2.666…
今回は小数第1位まで答えるので、答え2.7秒
解答(2)船が岸壁から離れていく場合
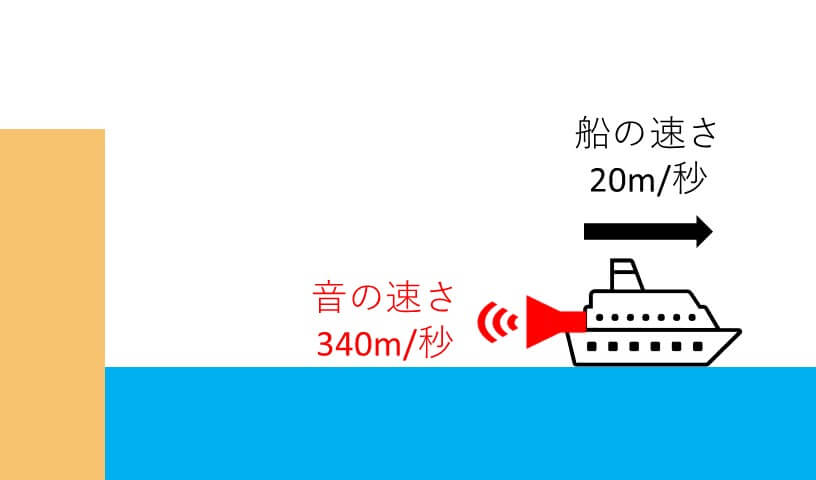
3秒後の位置を作図
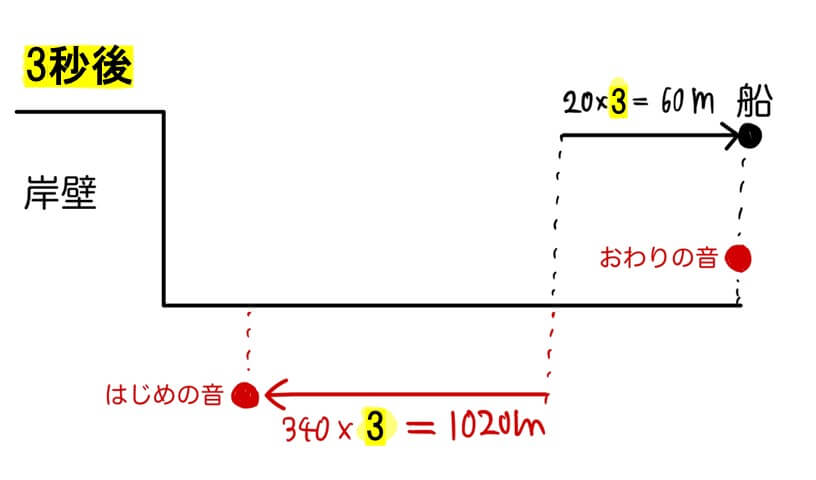
(1)同様、汽笛を鳴らして3秒後の「船」「はじめの音」「終わりの音」の位置関係を作図します。
船は岸壁から離れていくので、音の長さ(はじめの音とおわりの音の距離)は、(1)のときよりも長くなります。
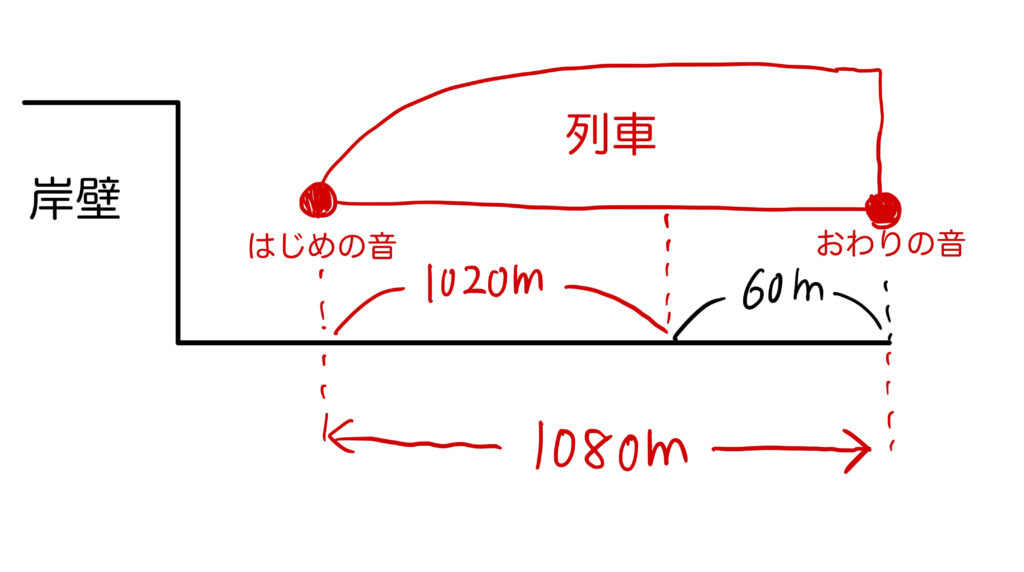
列車と船の通過算(追い抜き)
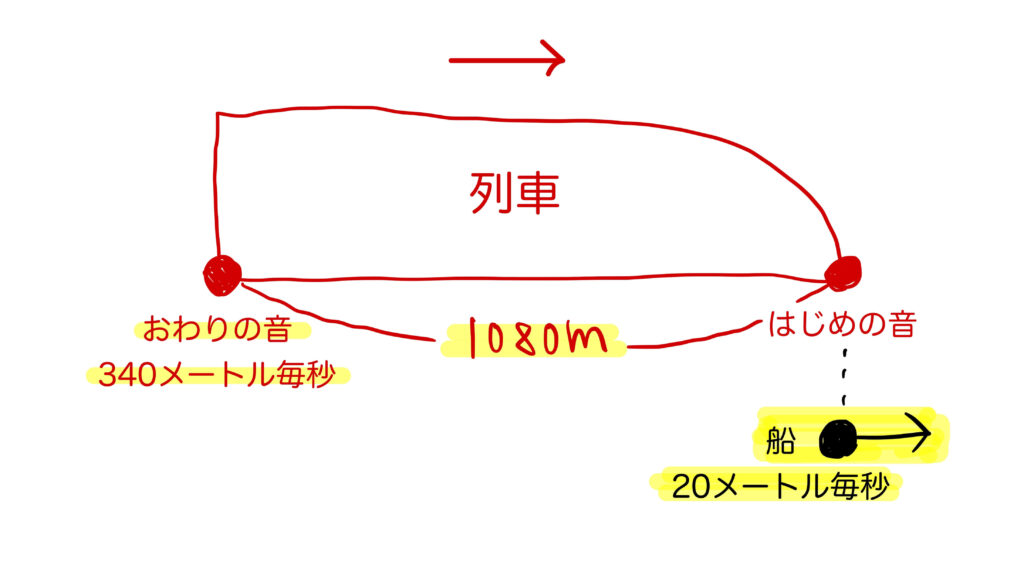
船が岸壁から離れていく場合、
「列車と見なした反射音(1080m)が船(0m)を追い抜く時間」=「船に乗っている人が反射音を聞いていた時間」
となります。
追い抜く時間=(列車の長さ+船の長さ)÷(列車の速さ-船の速さ)なので、
(1080+0)÷(340-20)=3.375
今回は小数第1位まで答えるので、答え3.4秒
まとめ|「音の長さ」を「列車」と見なせば通過算
一見すると難しそうな問題ですが、はじめの音からおわりの音までの「音の長さ」を「列車」と見なすことで、「列車と船がすれちがう通過算」と見なすことができます。最後にポイントを載せておきます。