旅人算とは?|「池のまわり」を移動する問題でよく出る!
旅人算の基本:速さ×時間=道のり
旅人算とは、「速さ・時間・道のり」の関係を使って、出発してから出会うまでや、追いつくまでの時間や距離を求める問題です。
まず覚えるべき公式は、基本中の基本:
速さ × 時間 = 道のり
この公式を使って、「どのくらい進んだか」「どのくらい時間がかかるか」などを計算します。
たとえば、
- 毎分80メートルで歩く人が10分歩けば → 80×10=800メートル進む。
- 500メートル進むのに、毎分100メートルなら → 500÷100=5分かかる。
といった具合です。
追いつく?出会う?2つのパターンを見分けよう
池のまわりの問題では、「AさんとBさんが同時にスタート」して――
- 同じ方向に進んでいる → 速い人が追いつく問題(追いつき算)
- 反対方向に進んでいる → どこかで出会う問題(出会い算)
という2パターンに分かれます。
✅見分け方のポイント:
- 同じ方向なら差が縮まる→追いつき問題
- 反対方向ならどんどん近づく→出会い問題
この2つをしっかり見分けることで、正しい式が立てられるようになります。
出会う場合|2人の道のりの合計が池1周分
例題1:出会い算|出会うまでの時間を求める
AさんとBさんが池のまわりを反対方向に向かって、同時にスタートしました。
Aさんは毎分80メートル、Bさんは毎分100メートルで歩いています。
出発してから□分後、2人はちょうどすれちがいました。
このとき、池1周の長さをどのように表せるでしょうか?
図で考える!2人が出会うまでの道のり
池のまわりをぐるっと1周するように、2人は反対方向に歩いています。
つまり、AさんとBさんが進んだ道のりを合わせると、ちょうど池を1周したことになるのです。
たとえば、Aさんが池の半分、Bさんがもう半分を進めば、2人は出会えますよね。
ここでのポイントは:
出会う=2人の道のりの合計=池1周分
という関係です。
線分図で関係を整理する
図にするとこんなイメージです:
スタート ←— Aさんの道のり(80×□) —→ ←— Bさんの道のり(100×□) —→
(出会った時点で、2人の合計移動距離=池1周)2人はすれちがうまでに、それぞれの速さで□分進んでいます。
式で表す|池1周=(速さの合計)×時間
2人が進んだ道のりの合計は:
Aさんの道のり+Bさんの道のり=(80×□)+(100×□)=(80+100)×□つまり、池1周の長さは
池1周=(速さの合計)× 時間
という式で表せます。
ポイントまとめ:出会うときは「合計=池1周分」
- 反対方向にスタートして出会うときは、2人がそれぞれ進んだ道のりの合計が池1周分になります。
- 式で覚えよう:
池1周=(Aの速さ+Bの速さ)× 時間
追いつく場合|速い人が池1周分多く走る
例題2:追いつくまでの時間を求める
AさんとBさんが、1周300メートル池のまわりを同じ方向に、同時にスタートしました。
Aさんは毎分80メートル、Bさんは毎分100メートルで走ります。
出発してからしばらくして、BさんがAさんにちょうど1回目に追いつきました。
追いつくまでの時間は何分でしょうか?
図で考える!Aさんの進んだ道のり
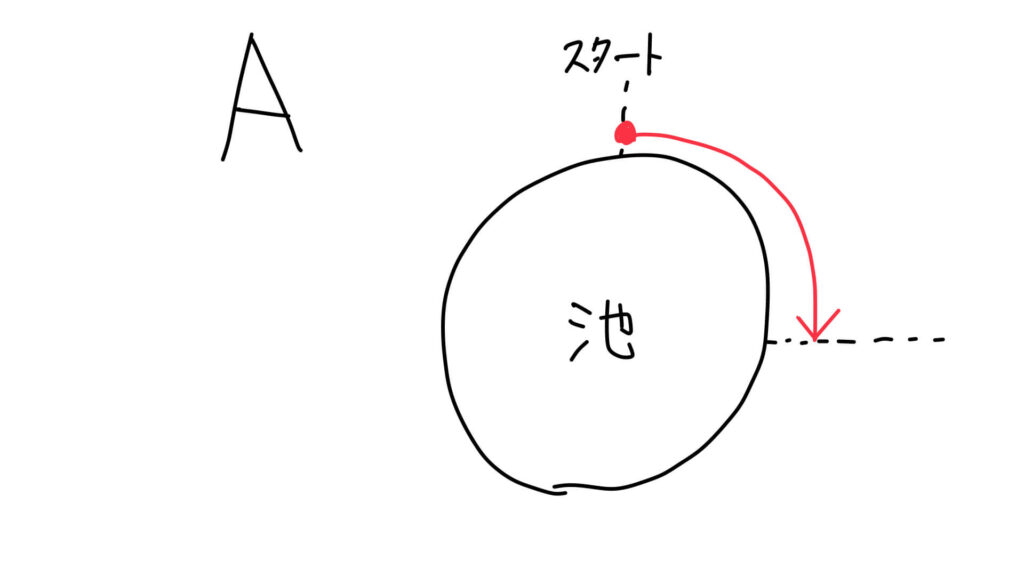
図で考える!Bさんの進んだ道のり
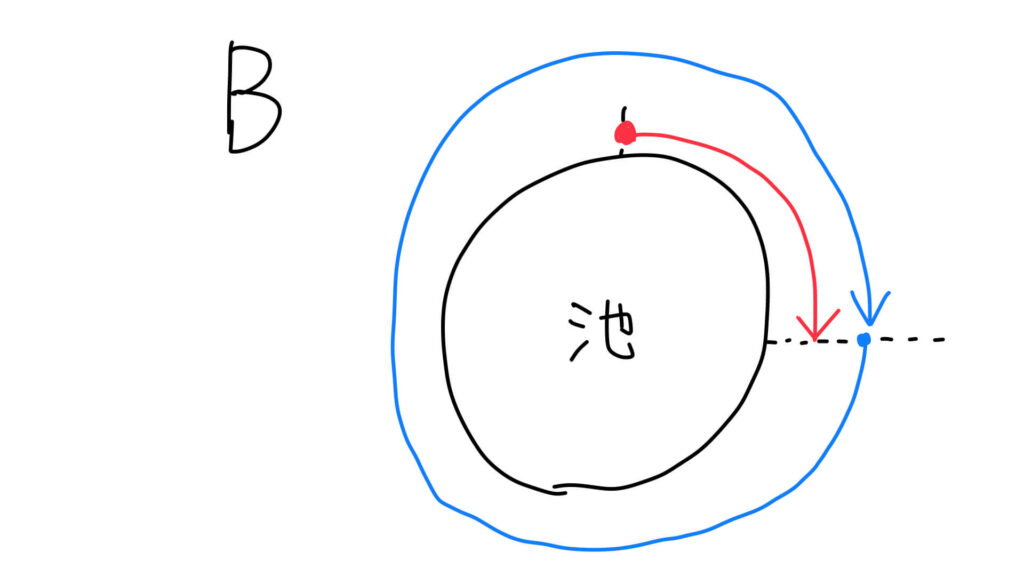
出発してから□分がたったとき、
- Aさんは「80×□」メートル進んでいます。
- Bさんは「100×□」メートル進んでいます。
このとき、BさんはAさんにちょうど1周分だけ多く進んでいます。
つまり、Bさんの道のりのほうが、池1周分だけ長いのです。
線分図で関係を整理する
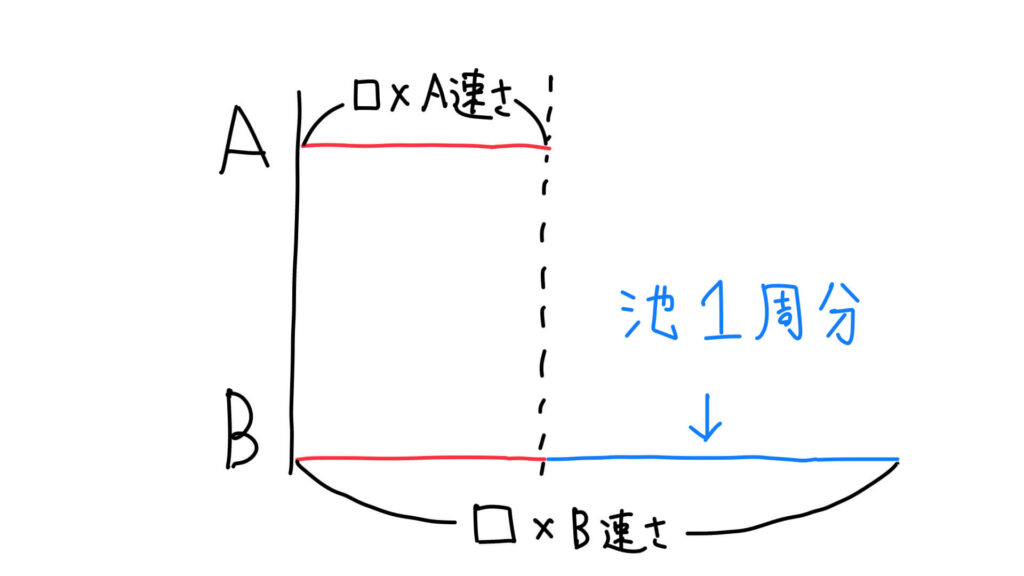
Aさんの道のり=80×□
Bさんの道のり=100×□このことから、池1周の長さは:
Bさんの道のり − Aさんの道のり
で表すことができます。
式で表す|池1周=(速さの差)×時間
では、式にしてみましょう。
池1周の長さ =(Bの速さ×□)−(Aの速さ×□)
300 =(100×□)−(80×□)
=(100−80)×□
= 20×□
よって、□=300÷20=15(分)つまり、
池1周(2人の移動距離の差)=速さの差× 時間
という関係式が成り立ちます。
ポイントまとめ:追いつくときは「2人の移動距離の差=池1周分」
- 同じ方向に出発して追いついたとき、
速い人が1周分だけ多く進んでいると考えよう! - 式にするときは、
速さの差 × 時間=池1周分 - 図や線分図をイメージすると、式の意味がよくわかります。
苦手な子におすすめ|旅人算を克服する家庭学習と指導方法
旅人算、とくに「池のまわりを移動する問題」は、多くの子どもがつまずく単元のひとつです。
しかし、コツをつかんで練習を重ねれば、必ず得意になります。
ここでは、ご家庭でできる学習法と、塾や家庭教師の活用法について紹介します。
家庭でできる復習ポイントと練習問題
まずは、家庭でできる復習から始めましょう。
✅ ポイント1:速さ×時間=道のりの公式を完全に身につける
旅人算は、この基本が理解できていないとどんな応用問題も解けません。
公式を見て覚えるだけでなく、簡単な数値で繰り返し計算練習をすることが大切です。
✅ ポイント2:図を描く習慣をつける
文章を読むだけではイメージがつきにくいので、
「何分でどれだけ進んだか」「どのくらい差があるか」などを線分図や円で図示させてみましょう。
✅ ポイント3:少しずつステップアップする
最初は反対方向に出発する「出会い算」から始めて、慣れてきたら「追いつき算」に挑戦しましょう。
1問1問、正しい式を立てられたかを確認しながら進めると、理解が定着しやすくなります。
個別指導や家庭教師でつまずきをなくす
苦手意識が強い場合は、塾や家庭教師での対話型の学習が効果的です。
一人で悩まず、質問できる環境があると理解がグッと深まります。
家庭学習でのサポートがむずかしいと感じる場合は、個別指導や家庭教師を検討してみるのも良い選択肢です。
- なぜその式になるのか
- どうやって図を描けばいいのか
- どこでつまずいているのか
こういった細かいポイントを、会話をしながら一緒に確認してくれる先生がいると安心です。
塾の個別指導や家庭教師では、子ども一人ひとりの理解度にあわせて説明を調整できるため、
「なんとなくわからない…」という状態から脱するのに最適です。


